UC San Diego Computer Science Researchers Shine at SIGGRAPH Asia 2025

Article Content

Congratulations to everyone involved in the two UC San Diego Center for Visual Computing papers honored at SIGGRAPH Asia 2025.

Best Paper Award at SIGGRAPH Asia 2025

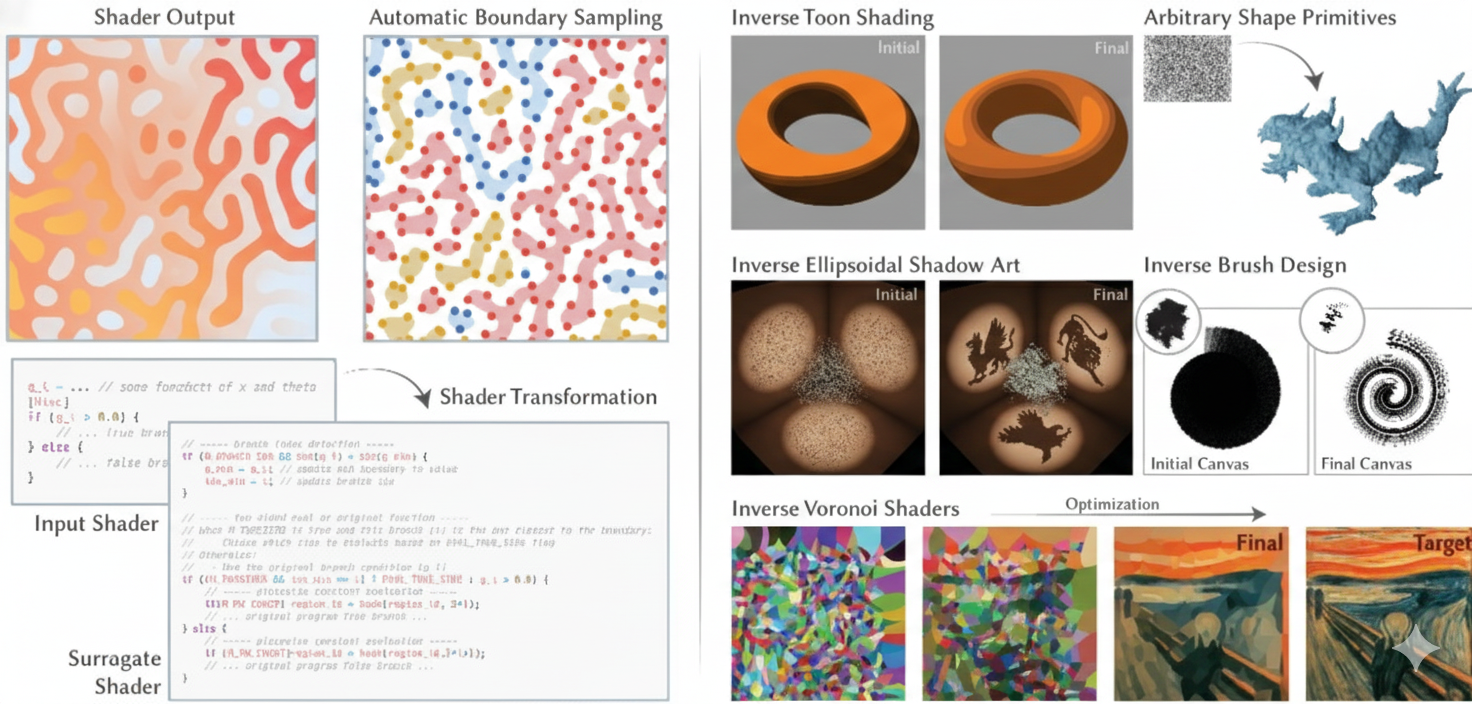
Automatic Sampling for Discontinuities in Differentiable Shaders

Paper Description: Many tasks in graphics and vision require computing derivatives of integrals of discontinuous functions, which have previously either required specialized routines or suffered from high variance. The team introduced a program transform and boundary sampling technique that computes accurate derivatives for arbitrary shader programs, enabling a range of applications such as painterly rendering, constructive solid geometry (CSG), rasterization, discontinuous textures, and more.

Watch the video here.

First Author:

• Yash Belhe (UC San Diego)

Co-Authors:

• Ishit Mehta (UC San Diego)
• Wesley Chang (UC San Diego)
• Iliyan Georgiev (Adobe Research)
• Michaël Gharbi (Reve)
• Ravi Ramamoorthi (UC San Diego, Director of the Center for Visual Computing)
• Tzu-Mao Li (UC San Diego)

Best Paper Honorable Mention at SIGGRAPH Asia 2025

Gaussian Integral Linear Operators for Precomputed Graphics

Paper description: In this work, we introduce a new approach to using integral linear operators for precomputed graphics that approximates both the kernel and the input function using Gaussian mixtures. This formulation allows the integral operator to be evaluated analytically, leading to improved flexibility in kernel storage and output representation. Moreover, this method naturally supports the sequential application of multiple operators and enables closed-form operator composition, which is particularly beneficial in tasks involving chains of operators. The researchers demonstrate the versatility and effectiveness of this approach across a variety of graphics problems, including environment map relighting, boundary value problems, and fluorescence rendering.

First Author:

• Haolin Lu (UC San Diego, formerly at D4, Max Planck Institute for Informatics)

Co-Authors:

• Yash Belhe (UC San Diego)
• Gurprit Singh (Max Planck Institute for Informatics)
• Tzu-Mao Li (UC San Diego)
• Toshiya Hachisuka (University of Waterloo)